Booth 算法
用于补码一位乘法
描述
- 这是一种有符号数的乘法,采用相加和相剪的操作计算补码的数据乘积,考虑$x*y$
- 设$[x]_补=x_sx_1x_2x_3…x_n,[y]_补=y_sy_1y_2y_3…y_n$
- 运算规则
- 符号位参与运算切都以补码的形式表示
- 被乘数一般取双符号位参与运算,部分积取双符号位,初值为0,乘数采取单符号位
- 乘数末尾附加$y_{n+1}$,初值为0
- 根据$(y_n,y_{n+1})$确定操作
- 移位按照补码右移规则进行(算数右移)
- 按照上述步骤进行n+1步,第n+1步不进行移位
算法的原理
- 基本思路:考虑一个一个数和一个连续的1的情况,如
- $M*(0011100)$
- $=M*(2^4+2^3+2^2)$
- $=M*(2^5-2^2)$
- 从而
- 10表示连续1的开始,对应$M*2^5$
- 01表示连续1的结束,对应$-M*2^2$
- 于是有移位的规则
| $y_n$ | $y_{n+1}$ | operations |
|---|---|---|
| 0 | 0 | 部分积右移一位 |
| 0 | 1 | 部分积$+[-x]_补$,部分积右移一位 |
| 1 | 0 | 部分积$+[x]_补$,部分积右移一位 |
| 1 | 1 | 部分积右移一位 |
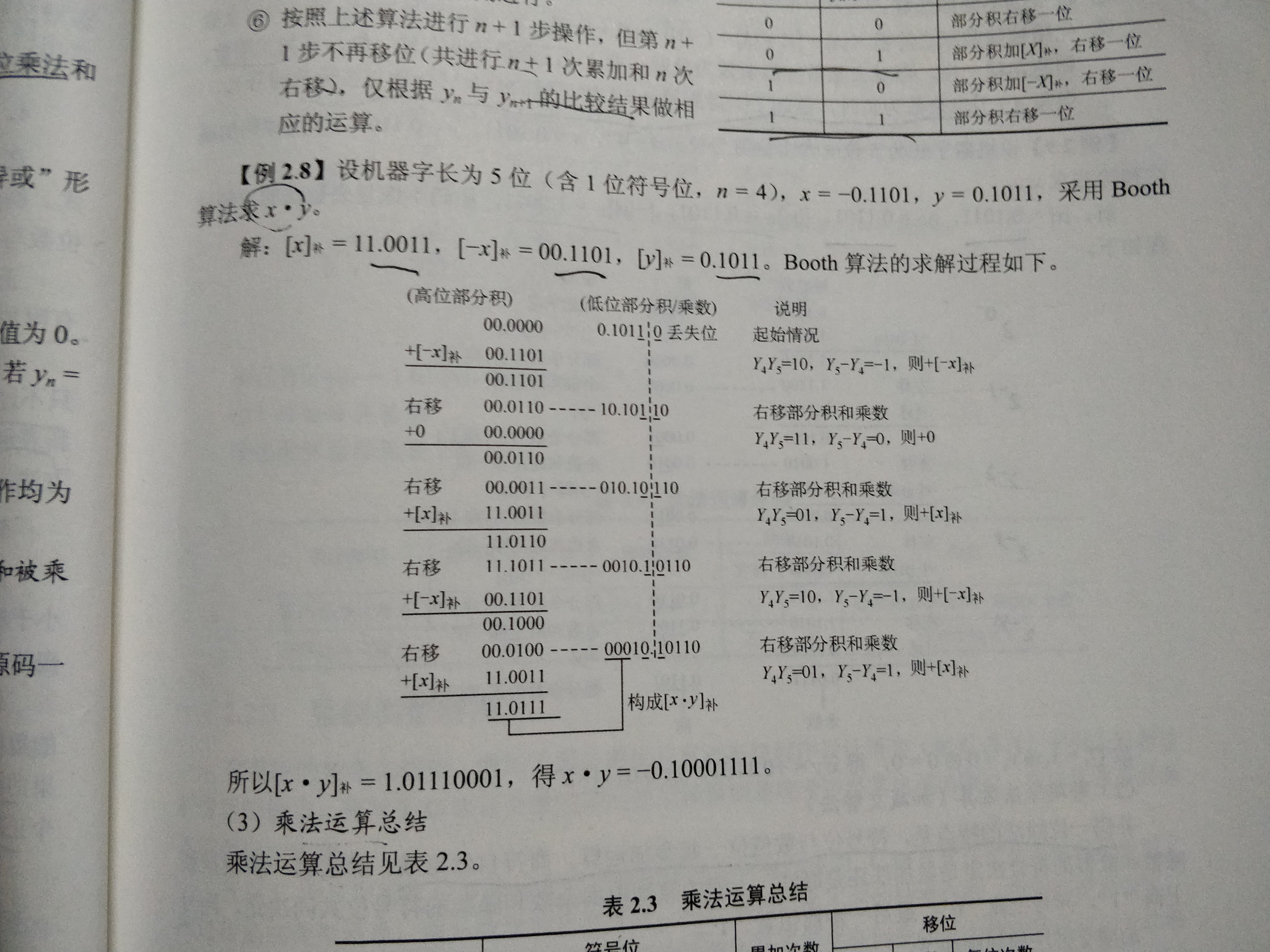
实例