约瑟夫环

Posted on | Edited on | In

Joseph Ping 约瑟夫环

问题描述

N个人坐成一个圆环（编号为1 - N），从第1个人开始报数，数到K的人出列，后面的人重新从1开始报数。问最后剩下的人的编号。

思路

  1. 直接模拟,复杂度O(n^2)
  2. 找规律

找规律

  1. 考虑N个人，最后一个出列的人的编号是p（从1开始编号）
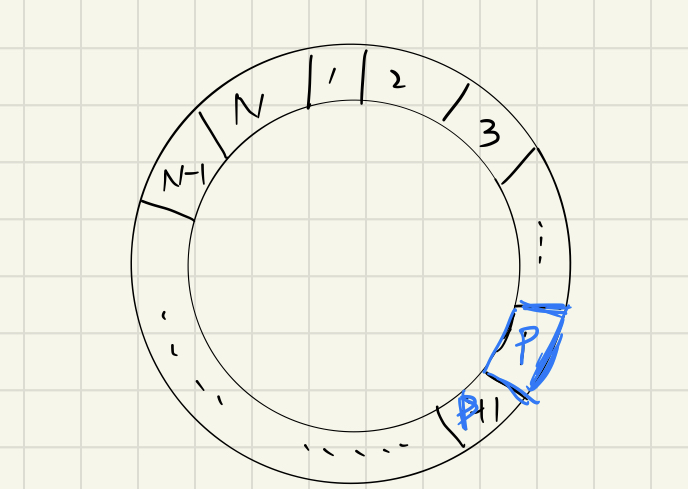
  2. 当有N+1个人时，第一个出列的人的编号是(K-1)%(N+1)+1
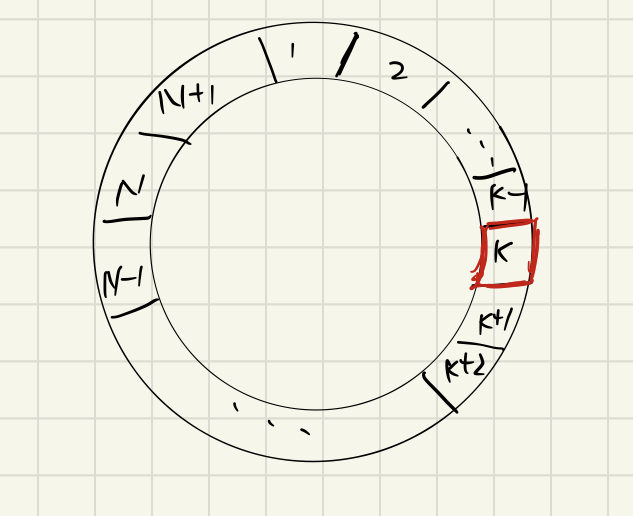
  3. 从第(K-1+1)%(N+1)+1个人开始重新编号（红色的部分）
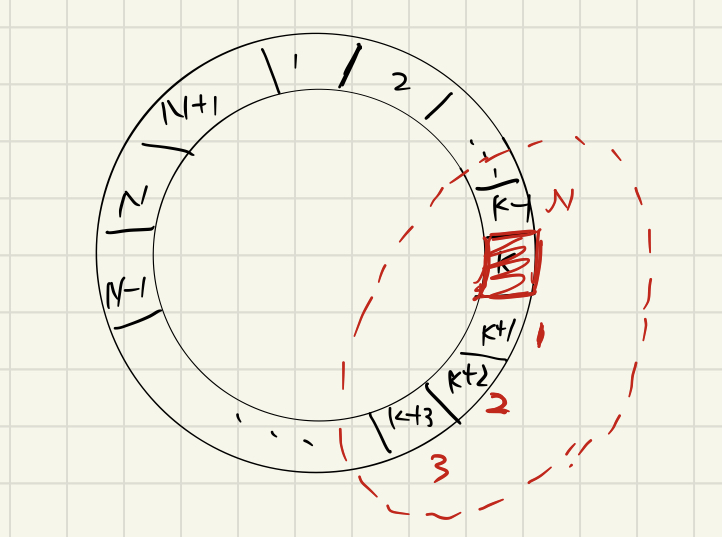
  4. 红色的编号和黑色的编号具有这样的关系：令红色编号i对应的黑色编号为j，则j=(i-1+K)%(N+1)+1
  5. 当第一个人走了以后，经过重新的编排（红色的编号）剩下的N个人满足1.的情况，根据4.的对应关系，则N+1个人时最后出列的人的编号是(p-1+K)%(N+1)+1
  6. 时间复杂度为O(n)

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#include <iostream>
using namespace std;
int n,k;

int find_1(int n,int k)//递归
{
    if(n==1)return 0;
    return (k+find_1(n-1,k))%n;
}

int find_2(int n,int k)//非递归
{
    int cn=1;
    int pos=0;
    while(cn<n)
    {
        cn++;
        pos=(pos+k)%cn;
    }
    return pos;
}

int main(){
    cin>>n>>k;
    cout<<find_1(n,k)+1<<endl;
    cout<<find_2(n,k)+1<<endl;
    return 0;
}